Содержание
Математика очень человечна: нам всем нравится думать, устанавливать связи и проверять, верны ли наши выводы. Эта дисциплина гораздо интереснее и разнообразнее, чем запоминание формул и выполнение вычислений. Это творческое начинание, которое продвигает общество и может сделать жизнь человека богаче и прекраснее. Математика помогает решать многие задачи из реальной жизни, используя только мозг.
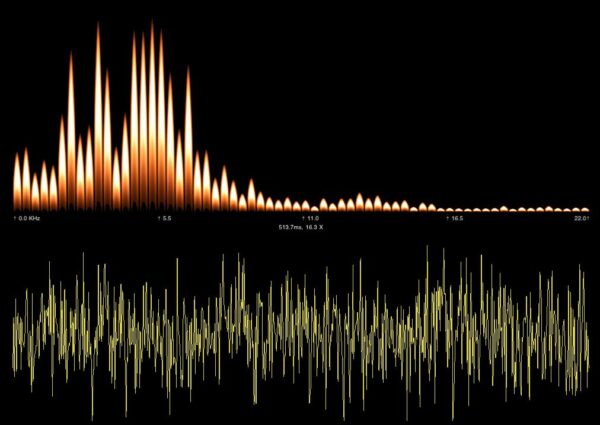
Что такое вейвлеты
Вейвлеты — это математические инструменты, которые очень полезны при анализе изображений и других сигналов, таких, как аудиофайлы, медицинские снимки или записи активности тела и даже рябь в самом пространстве, созданную мощнейшими астрономическими событиями во Вселенной. С 1980-х годов математики, инженеры и физики одновременно изучали вейвлеты. Это было захватывающее время, поскольку было ясно, что каждая область рассматривает одну часть общей концепции, которая будет чрезвычайно полезна в нескольких областях. Как следует из названия — это небольшие волны, которые могут принимать различные формы.
Вейвлеты конечны — это означает, что их значение отлично от нуля только в определённой области пространства. Каждый из них можно растянуть или сжать, чтобы сделать его уже или шире, а также можно сместить влево или вправо по оси X, чтобы он соответствовал анализируемому сигналу. Проще думать об этом явлении, как о строительных блоках, с помощью которых можно реконструировать и анализировать сигналы и изображения.
Прикладное применение
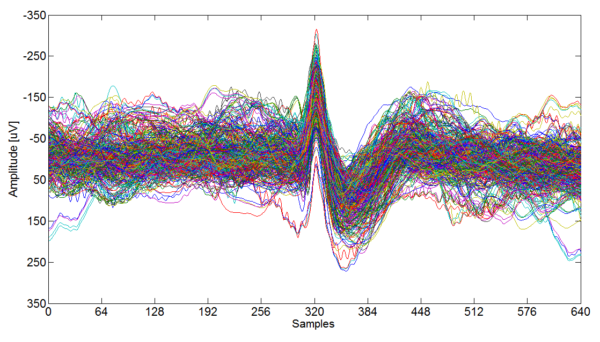
В прикладном плане, учёные объясняют назначение этих функций так: «Когда у нас есть сигнал или изображение, которое мы хотим проанализировать, мы можем выяснить, какие вейвлеты наиболее похожи на паттерны (шаблоны) в сигнале. Важно отметить, что мы можем масштабировать эти волны: увеличить, чтобы увидеть более мелкие детали сигнала (сжать вейвлет) или уменьшить, чтобы получить более широкий обзор (растянуть). Затем, используя некоторые математические приёмы, можно их использовать для получения конкретной информации из сигнала или изображения, например, содержит ли оно определённую форму или шаблон, который мы ищем. Либо сжать его — то есть сохранить изображение, используя лишь небольшую часть исходного пространства памяти, которая по-прежнему даёт достаточно информации. То есть, говоря простыми словами, эти элементы используются для анализа закономерностей в сигналах и изображениях.»
Изображение в цифре
Изображения представляются в компьютерах как наборы чисел. Для цифрового изображения в оттенках серого цвет каждого пикселя представлен одним числом, в диапазоне от 0 до 255. Число 0 представляет чёрный цвет, а 255 — белый. Все числа между ними представляют собой различные оттенки серого. Если изображение цветное, в формате RGB, то используется три числа для обозначения трёх компонентов цвета — красного, зелёного и синего. Компьютеры представляют всю информацию, используя только два состояния: «0» или «1». Каждый такой элемент называется битом, и каждый бит может представлять только одно из этих состояний. Если объединить два бита, поскольку каждый из них может независимо представлять два состояния, оба они вместе могут представлять уже квадрат двойки — то есть четыре возможных варианта. Чтобы представить 256 чисел (от 0 до 255), то потребуется система из 8 бит (два в восьмой степени). И уже в таком формате можно представить цвет каждого пикселя для изображений в градациях серого или в системе RGB (восьмибитная глубина цвета). Существуют другие системы представления цвета — так, например, в полиграфии, цвета представлены в системе CMYK (голубой, пурпурный, жёлтый и чёрный). Но там уже градация по каждому цвету идёт в процентном отношении от 0 до 100 единиц каждого цвета.
Типичное прямоугольное цифровое изображение на мониторах прежнего поколения состояло из 512 строк, каждая из которых имела 512 пикселей, поэтому требовалось 512 512 = 262 144 пикселей в целом. Каждый пиксель представлен 8 битами, поэтому требовалось 262 144 8 = 2 097 152 бита, или единицы информации, чтобы представить только одно типичное изображение в оттенках серого (для цветных изображений нужно было в три раза больше)! Сейчас уже мониторы стали более продвинутыми, и стандарты изображения разные. Одним из самых распространённых является 1920 пикселей, на 1080. То есть и информации для одного кадра таких изображений на мониторах требуется ещё на порядок больше. Это огромный объем информации, особенно если подумать о фильмах, в которых имеется 25 изображений в секунду (а сейчас устройства снимают с частотой 30 и даже 60 кадров в секунду), каждое из которых представлено миллионами бит.
Теперь вам наверняка становится понятно, почему видеокарты, с их специализированными чипами, настроенными на быстродействие, зачастую используют в серверах для скоростных вычислений (майнинга, например). Часто приходится находить способы уменьшить объем компьютерной памяти, необходимой для хранения изображений, без потери важной информации — это называется компрессией (или сжатием). Для этого пытаются сжать изображение и уменьшить количество пикселей, хранящихся в памяти. Простой способ сделать это — взять каждые два соседних пикселя изображения, вычислить среднее количество их цвета и сохранить только один пиксель с этим средним числом цвета. При этом уменьшается количество пикселей изображения в два раза по горизонтали (для соседних пикселей в каждой строке) и в два раза по вертикали (для соседних пикселей в каждом столбце). Можно повторять этот процесс много раз и создать очень маленькое изображение.
Но когда проводится такое усреднение, то теряется важная информация, которая содержалась в исходном изображении — без неё реконструированное изображение может сделаться более размытым. Если мы не хотим потерять эту информацию, мы должны убедиться, что можем восстановить исходное изображение из усреднённого. Для этого также сохраняется разница между исходными пикселями, которые были усреднены, потому, что исходные числа можно найти по среднему значению и разнице двух чисел. Оказывается, можно представить эти средние значения и различия с помощью вейвлетов! Если принять средние значения и различия только между двумя близкими соседями, то можно получить вейвлет, похожий на лестницу (вейвлет Хаара). Часто хочется объединить более крупные группы соседних пикселей, а это значит, что каждый усреднённый пиксель будет содержать больше информации. Если это сделать, то получатся другие вейвлеты, которые будут более гладкими.
Как Вейвлеты оптимизируют изображения
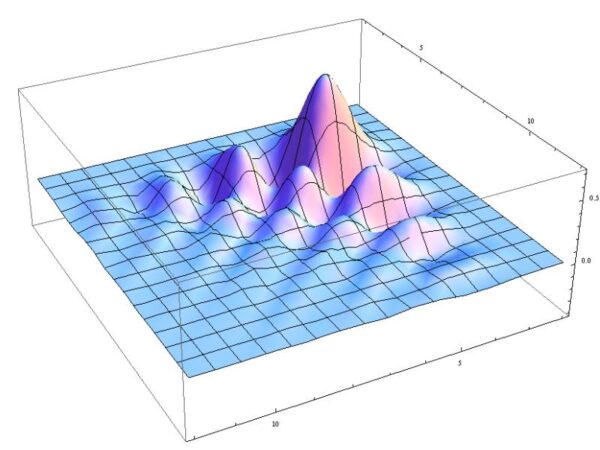
Вейвлеты могут показать специалистам наиболее важные части изображения, то есть области изображения, где «что-то происходит», например, границы силуэта или лица. А могут дать информацию об общих тенденциях значений пикселей изображения, также о горизонтальных, вертикальных и диагональных деталях или резких изменениях цвета. Эти функции лучше анализируют резкие изменения изображений (и других сигналов) по сравнению с другими распространёнными методами анализа. Такой подход позволяет идентифицировать и сохранять только важные особенности изображения, где есть большие изменения, и отбрасывать информацию об однородных участках. Информации, которая сохраняется после обработки, достаточно, чтобы можно было восстановить довольно точную версию исходного изображения (помните, как в фильмах компьютерщики-полицейские делают чётче размытое изображение с видеозаписи?). Сохранения всего 10% или даже 3% исходных данных часто бывает достаточно, чтобы восстановить довольно хорошую версию исходного изображения.
Новые разработанные вейвлеты, специально для изображений, теперь применяются в новом методе компрессии, который называется стандартом сжатия JPEG2000, который широко используется для сжатия изображений высокого разрешения, во многих интернет-приложениях, в современных играх и для цифровых фильмов. В принципе, этот мощный инструмент можно использовать в любой ситуации, для которой требуется анализ сигналов, в том числе в области астрономии (для автоматического выбора наиболее сфокусированных изображений астрономических объектов), в криминалистике (для обнаружения манипуляций с цифровыми аудиофайлами, изображениями и видео), в медицине (для выявления заболеваний, вызывающих нарушение кровоснабжения сердца) и много где ещё. Технологии стремительно завоёвывают множество областей нашей жизни, а значит везде устанавливается всё больше и больше датчиков. Следовательно, собирается и больше данных, а значит вейвлеты будут играть ещё большую роль во многих приложениях.
В настоящее время учёные используют обозначенные методы для интересных и, возможно, весьма неожиданных приложений. Например, в одном из проектов они применяются для работы в области искусствоведения, для анализа картин и понимания их истории. В частности, учёные пытаются получить наилучшее представление о скрытых слоях, называемых подмалёвком, которые находятся под видимым наружным слоем краски. Под некоторыми картинами (привести в пример можно «Клочок травы» Ван Гога), находятся другие картины, называемые подмалёвками. После того, как подмалёвок выявляют с помощью рентгеновских лучей, посредством применения вейвлетов «обнажают» детали и максимально точно реконструируют подмалёвок в виртуальной визуализации. Также можно использовать этот метод для других приложений в искусстве, в таких, например, как изучение и удаление/создание трещин (кракелюров) в цифровых изображениях или омоложение состаренного цвета красок на картинах.